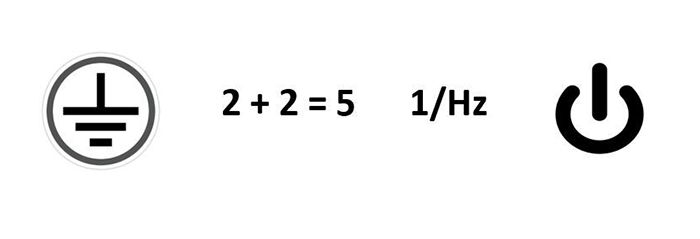1. Teknikrebus

The solution to this puzzle is a Swedish noun for a technical product that is now available in many Swedish homes. As in crossword puzzles, you may have to let your mind run free and not interpret the details too literally.

2. Cultural heritage and sauna energy

A world heritage site can be, for example, buildings, environments and natural areas. They are on a list published by Unesco. In Sweden, there are 15 world heritage sites, including Engelsberg’s mill, Hansestaden Visby, Grimetons radio station and the rock carving area in Tanum. International World Heritage Sites include the Pyramids of Egypt and the Yellowstone National Park.

There are also so-called intangible cultural heritage which, among other things, includes customs. In December 2020, Unesco included the Finnish sauna culture on its list of intangible cultural heritage. ”

The sauna culture in Finland is an integral part of the majority of the Finnish population. It contains so much more than just a hygienic aspect. In a sauna, you cleanse both body and soul and get a feeling of inner peace “, writes Unesco in a statement.

Other new choices on the list are the dish couscous, Venetian glass beads from the island of Murano and the art of watchmaking in France and Switzerland. In Sweden, which in 2011 signed the Convention for the Safeguarding of Intangible Cultural Heritage, the government has for fear of value hierarchies refrained from nominating Swedish proposals for intangible cultural heritage to the UNESCO International List. Possible candidates would otherwise be smorgasbord and Lucia trains.

Now back to the sauna. To heat it, you have to add energy. Where does this energy end up? It is perhaps natural to think that it is in the warm sauna air. But the surprising answer is that the energy in the air inside the sauna is about the same both when the sauna is cold and when it is hot.

Instead, the supplied energy ends up in the sauna walls and in the air outside the sauna. Can the reader explain it? The simple solution is based on the general gas law pV = NkT which provides a connection between the pressure p in a mass of gas with the volume V, the number of molecules N in the gas, Boltzmann’s constant k and the thermodynamic temperature T (expressed in kelvin).

3. Emptying of gravel pits

This mini-problem is about emptying a finite resource – namely a given gravel pit. Suppose we start the withdrawal in 2021. At first it is very small. In 2021, only 0.1 percent has been taken out. With the same withdrawal continued, it would be enough for 1,000 years. But we assume that withdrawals increase steadily by 7 percent annually.

According to the very useful 72 rule (more on that in the solution), this means a doubling of the annual withdrawal of about ten years. The following table shows what percentage of the gravel pit remains over the next 30 years at a 7 percent annual growth rate.

2021 99.9

2030 98.6

2040 95.9

2050 90.6

It seems to be a reassuringly slow withdrawal. When is the entire gravel pit emptied?

Solutions

1. Teknikrebus

The answer is “earth fault circuit breaker”. First comes the symbol for ground connection (“ground”) in an electrical circuit. 2 + 2 = 5 is “wrong”. The frequency unit hertz indicates number per second; 1 / Hz = 1 / hertz = ”s” (seconds).

According to the international standard IEC (International Electrotecnical Commission) 60417-5009, the last symbol refers to a standby state, ie a dormant state. It does not completely disconnect the device from the power supply, but is often popularly called a switch or, as in our rebus, “switch”.

A vertical line is according to IEC 60417-5007 a start symbol or a switch that means that the equipment is placed in a fully live position.

A circle is according to IEC 60417-5008 the symbol for shutdown, ie the power is completely disconnected from the unit. The symbol in the puzzle can thus partly be regarded as a combination of the symbols 5007 and 5008.

2. Cultural heritage and sauna energy

The solution can be briefly formulated by decreasing the number of gas molecules N at the same rate as the temperature T increases. The pressure p is everywhere inside the sauna the same as in the air outside. (More about this below.) Let the sauna’s full volume be V. Then it becomes pV = NkT constant, regardless of the temperature T. For a complete argument, one must know that the kinetic energy (translation and rotation) of each gas molecule is proportional to T.

The total energy in the air is then proportional to the NT. But now the temperature in the sauna varies, with at least T near the floor. Then we can imagine the volume in the sauna divided into parts with a certain fixed volume. In each such part is pV, and thus NT, constant.

The gas pressure is the same in all parts of the sauna, otherwise it would “blow” inside. No sauna is completely tight, and the air pressure on both sides of the sauna door is the same. When the sauna is heated, therefore, gas molecules will “leak out” to the environment. If you throw a bath, ie pour water on the stones of the sauna heater, the gas vapor is quickly formed.

It increases the gas pressure inside the sauna. In a small villa sauna, the sauna door immediately flies up slightly, so that pressure equalization can take place. The National Board of Housing, Building and Planning’s building regulations state that a sauna must be designed so that it can be evacuated quickly. The door must be outward-facing or of the pendulum type. The door must not have a lock and the door leaf must not be able to get caught in the frame due to thermal expansion or the influence of moisture.

If these demands had been met in the 1970s, a tragic fatal accident at Chalmers would have been avoided. At lunchtime, a technician went in to bathe. The door locked and the person was found dead after several hours.

That the total kinetic energy of the two-atom oxygen molecules and the nitrogen molecules is approximately 5kT / 2 follows from the so-called equipartition theorem. This is not the same energy as for the monoatomic noble gases or multatomic molecules such as carbon dioxide, but they only contribute insignificantly to the energy of the air.

3. Emptying a gravel pit

The surprising answer for many is that although only about 9 percent has been taken out during the first 30 years, the entire gravel pit has been emptied after just over another equal period of time (in 2083). The following table shows the remaining percentage for the years 2060–2080.

With good approximation, the total withdrawal for a certain period of time is equal to the withdrawal during the next doubling period of about ten years. For example, according to the table, 20 percent was taken out in 2060 and 40.7 percent in 2070. (After a “long” time, the rule applies exactly. We refrain from showing it here.)

This means that if it is half-emptied at a certain time, it is completely emptied after the next doubling time, in our case about ten years. If you then want to continue to extract gravel at the same rate of increase, you must find a gravel pit as large as the original for the next decade, and even that will only take ten years.

The example shows that the seemingly slow growth during the first period of an exponential course is soon replaced by a catastrophic increase.

So to the 72 rule. It says that if something increases with p percent per year, there is a doubling after about 72 /p year. On the border with very little p is the result 100ln (2) /p = 69.31… /p. (It is not difficult to prove mathematically.)

That the practical rule uses the number 72 and not 69 or 70 is due to the fact that 72 has many integer factors and that it is therefore often easy to calculate 72 / in your head.p. The table shows the doubling time in number of years at p percent annual change, partly according to the 72 rule and partly with a more accurate calculation.

We see that the rule initially slightly overestimates and then somewhat underestimates the doubling time, but it is remarkably accurate for “normal” rates of increase. Note that here and in the calculations above we have assumed that the increase refers to the end of each year and not continuously. Given that the 72 rule itself is an approximation, the difference between these two ways of calculating is not significant.

If you want to impress your surroundings, you can quickly make the following comment when someone, for example, says that the rate of increase is 8 percent per year. “That means a doubling in 9 years.” You do not need to reveal that you only did the main calculation 72/8 = 9. The rule applies just as well when reducing with p percent per year. Then the value is halved after approx. 72 /p year.